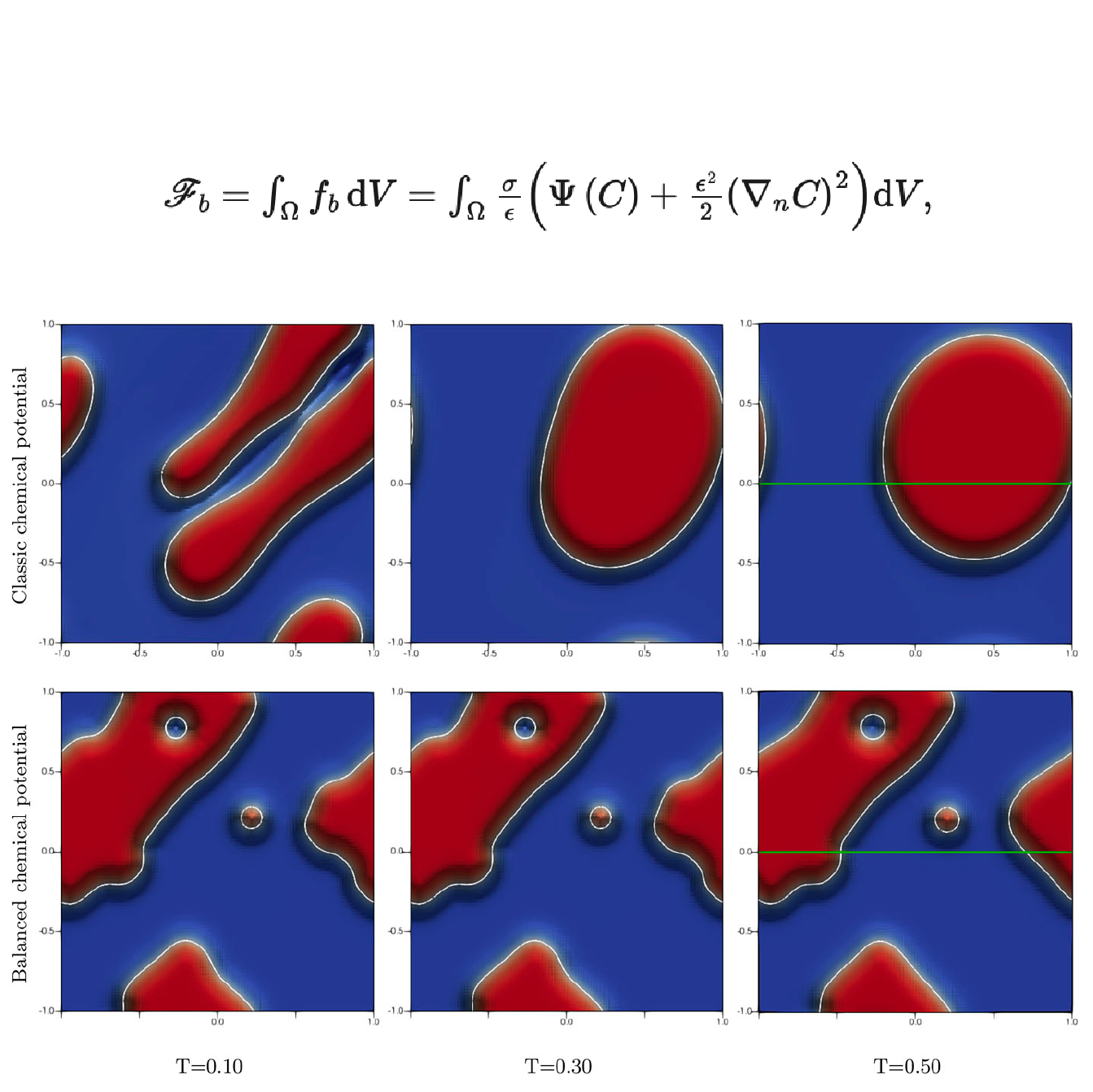
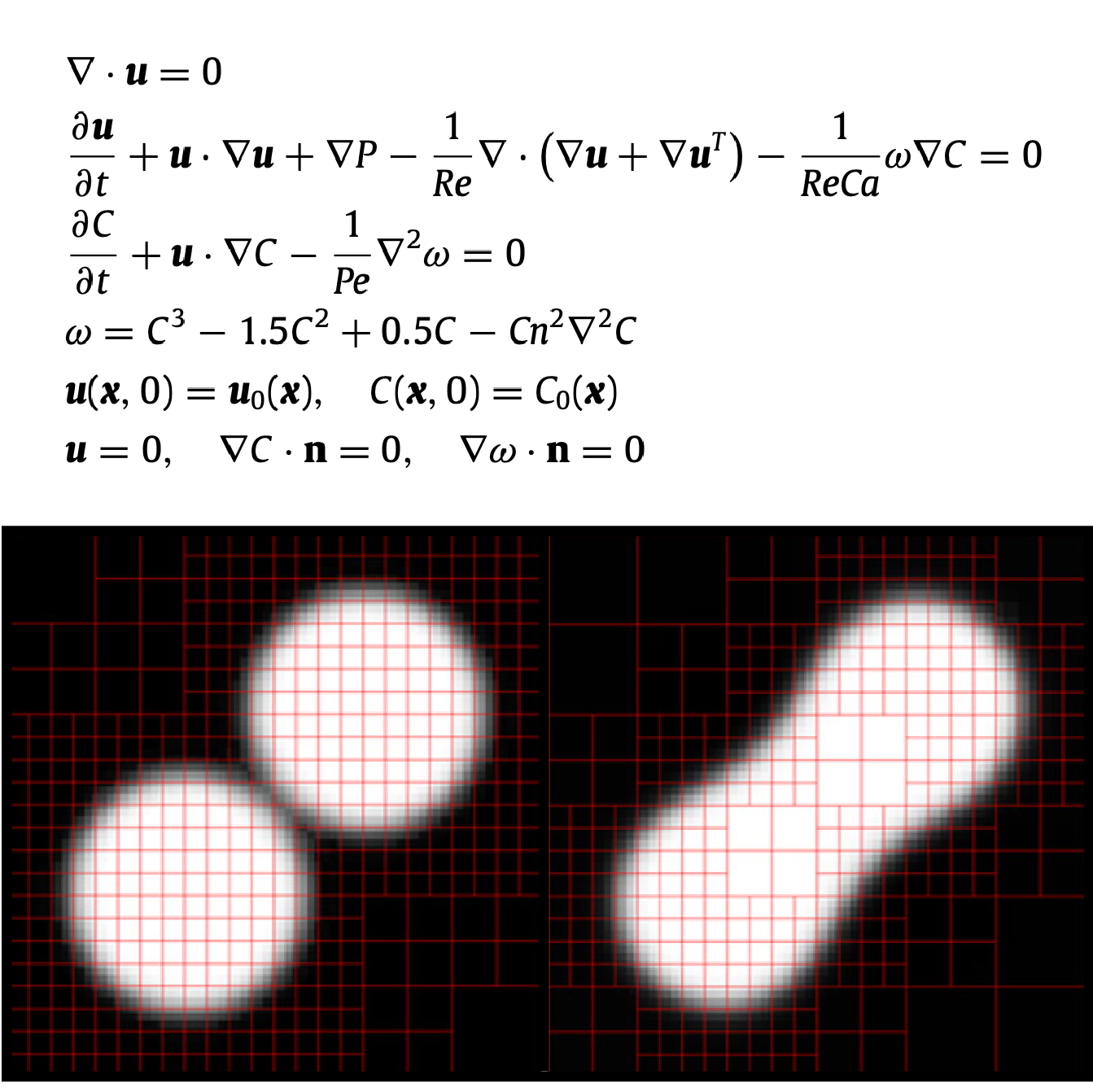
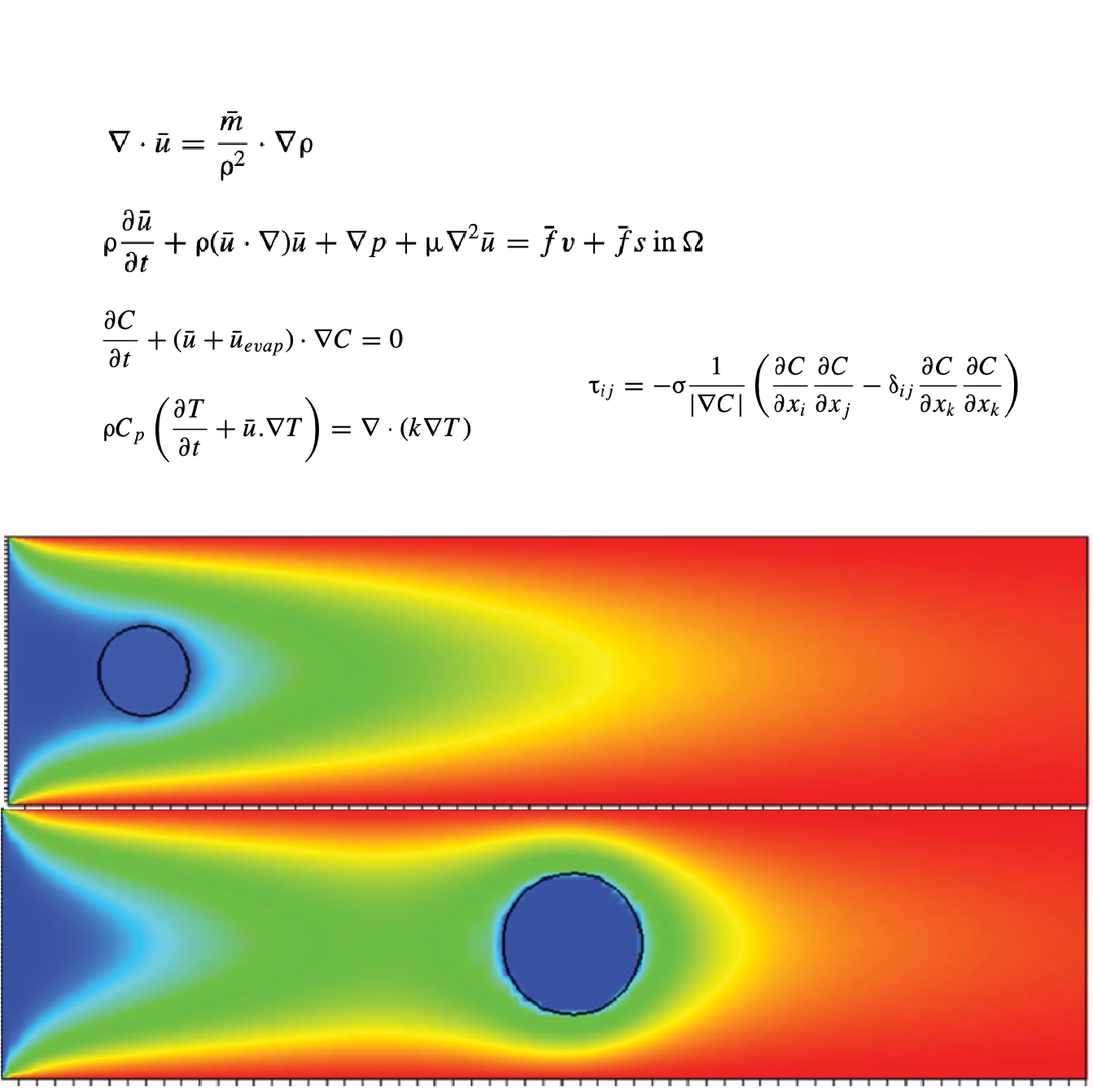
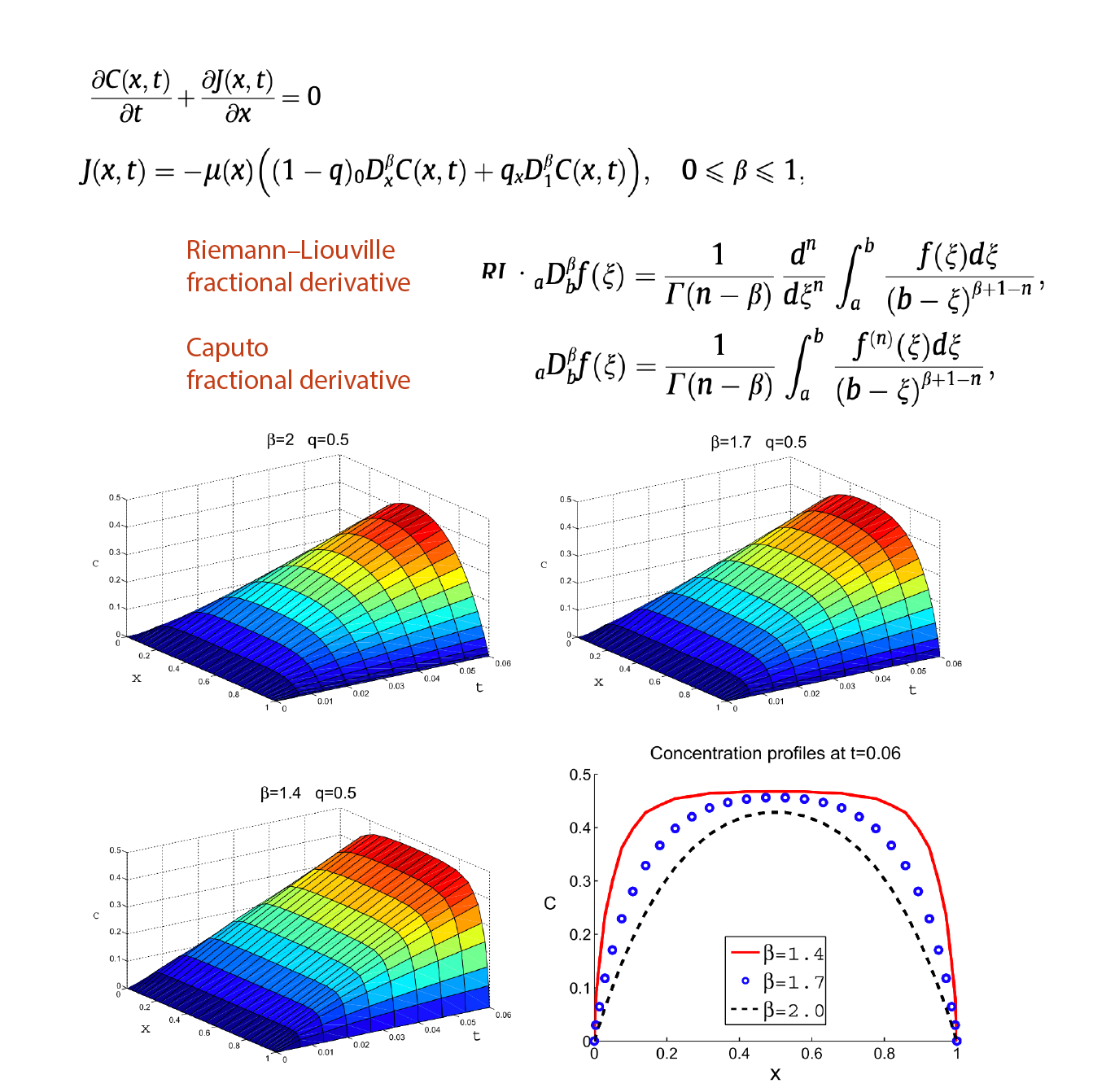
Numerical Methods for Interfacial Flows

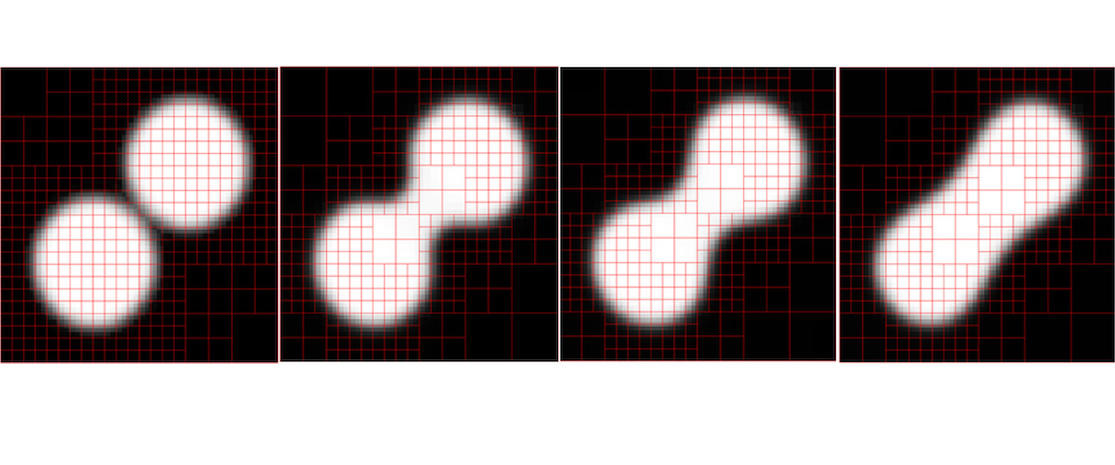
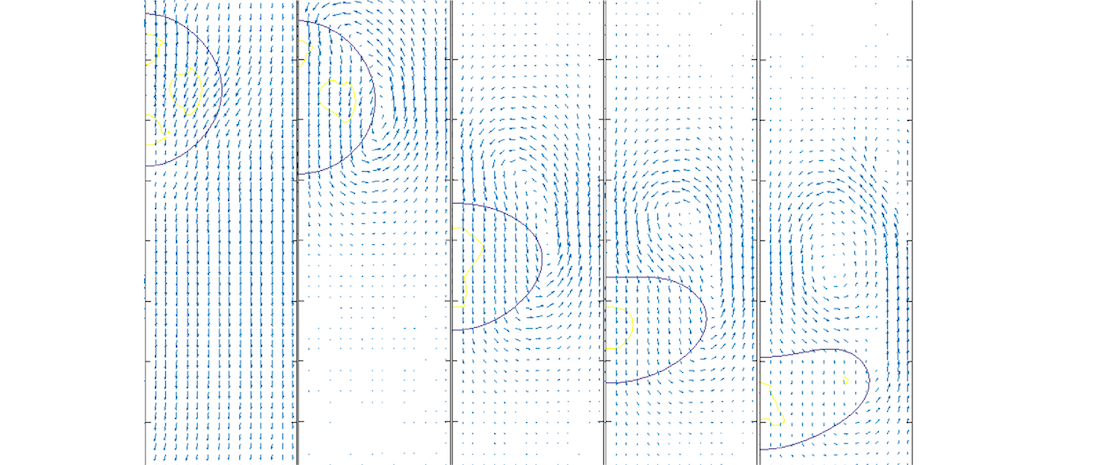
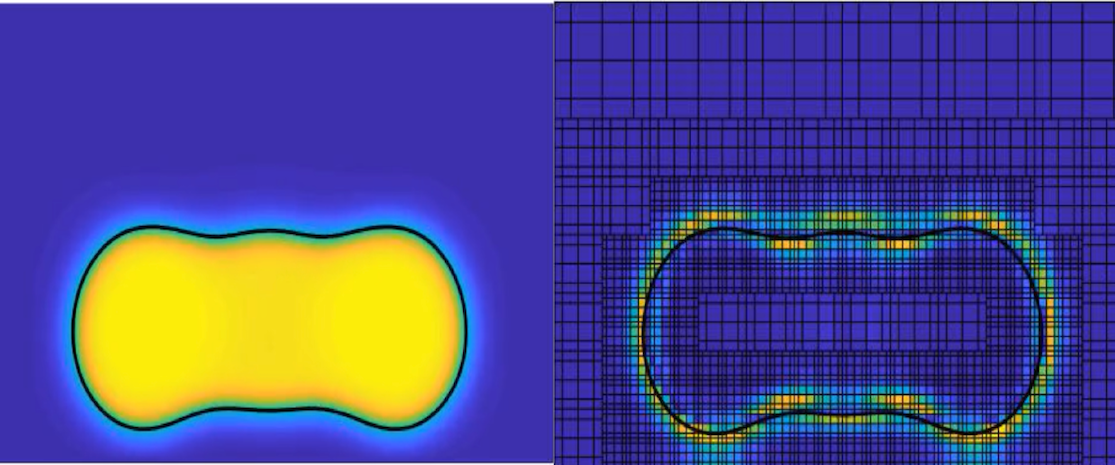
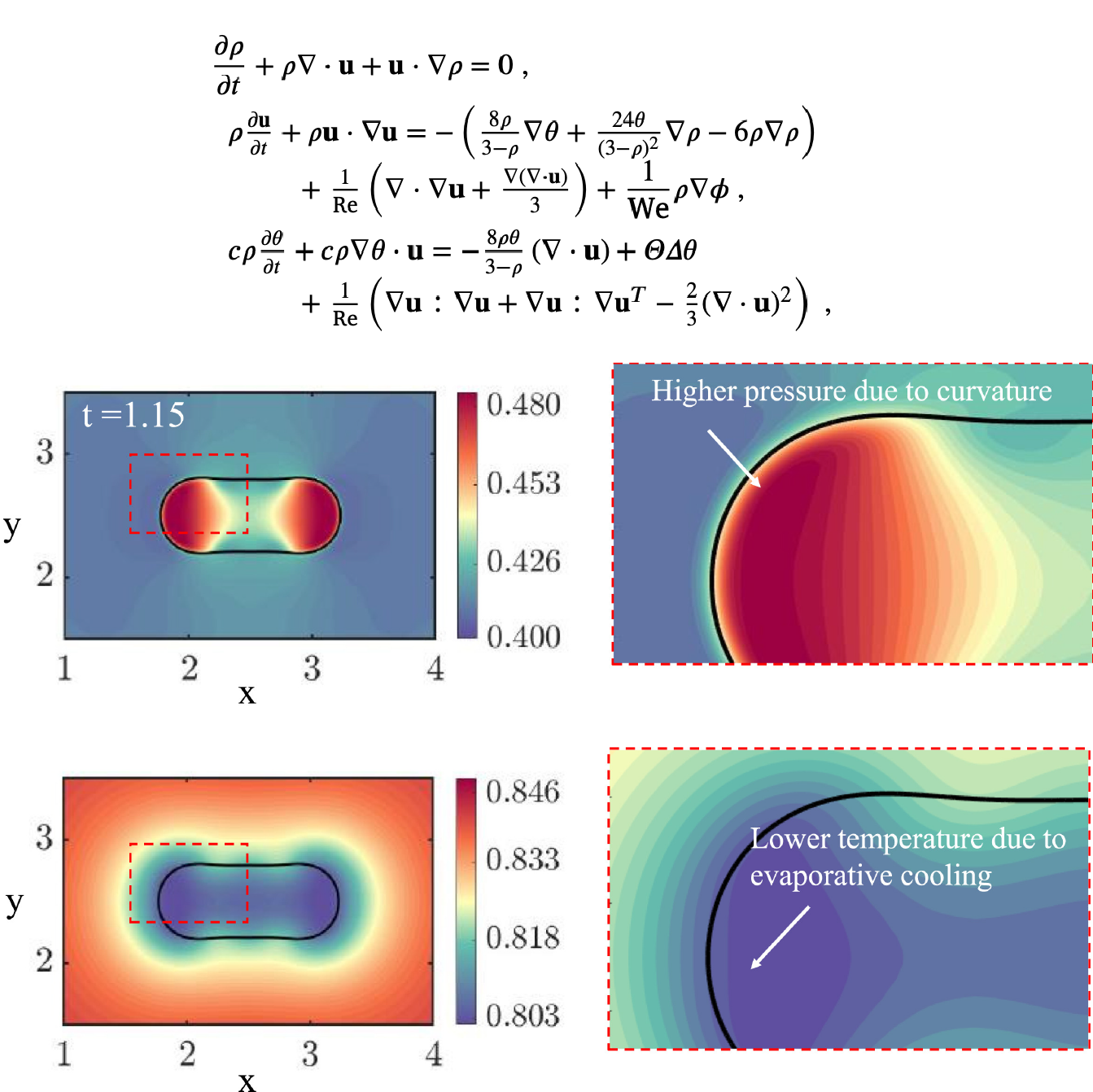
Numerical simulation of two-phase flows presents challenges such as representation of moving interfaces, fluid properties changing abruptly in a short length scale, surface tension effects difficult to capture numerically and the multiscale problem related to fluid-solid interaction near contact lines. Phase change phenomena such as evaporation and condensation add complexities to the problem. Our research focuses on diffuse interface methods for studying interfacial flows with phase change. In particular, we work with the Navier-Stokes-Korteweg model, which considers the fluid density as the phase-field parameter for identifying the liquid and vapor phases. The model handles compressible two-phase flow dynamics through van der Waals’ gradient theory along with a non-convex equation of state, which endows capillarity effects and phase transformation without ad-hoc assumptions on the gas-liquid interface. With this model we investigate heat and mass transfer processes during evaporation and condensation of droplets, trying to understand how local changes of the interface curvature and local thermodynamic conditions affect the phase change phenomena. The Navier-Stokes-Korteweg model is solved numerically by our in-house Least Squares Spectral Element Method simulation code. The code is a multi-purpose simulation platform including high order C0 Lagrangian interpolant polynomials, and C1 third order Hermite functions extended with bubbles functions. A non-conforming adaptive mesh refinement strategy using mortar elements is used to achieve the necessary resolution at fluid interfaces. The final system is solved by a parallel element-by-element CG or alternative direct solvers.

 
 

 

In this study, we show that local interface temperature variations are mainly due to evaporative cooling, and that the new temperature influences local mass flux during the evaporation of deformed droplets. We employ direct numerical simulations through the thermally coupled Navier–Stokes–Korteweg model – a diffuse interface model grounded in van der Waals square-gradient theory – and a space–time least-squares spectral element method in two dimensions. With this model, we effectively capture the dynamics of the droplet and its interface, accounting for droplet deformation and evaporative cooling effects.

Vitor H.C. Cunha, Julián N. García Hahn, Carlos A. Dorao, Maria Fernandino (2024). Investigation of the effect of curvature on the local mass flux of evaporating droplets using a phase field method, International Journal of Multiphase Flow. 174, 104771

 

In this work, a redefined energy functional is presented, which ensures a proper energy balance. While avoiding the nonphysical bulk diffusion, it achieves conservation of (enclosed) mass as well. Furthermore, overall system dynamics remain comparable to the classic energy functional. The redefined energy potential is still able to model spinodal decomposition, while it matches sharp interface results better when applied to a two-phase system.

Kwakkel M., Fernandino M., Dorao C.A. (2020). A redefined energy functional to prevent mass loss in phase-field methods. AIP Advances 10, 065124.

 
 
 
 
 

 

In this work, a C1 continuous h-adaptive mesh refinement technique with the least-squares spectral element method is presented. It is applied to the Navier– Stokes-Cahn–Hilliard (NSCH) system and the isothermal Navier–Stokes–Korteweg (NSK) system. Hermite polynomials are used to give global differentiability in the approximated solution, and a space–time coupled formulation and the element-by-element technique are implemented.

Park K., Gerritsma M., Fernandino M. (2018). C1 continuous h-adaptive least-squares spectral element method for phase field models. Comp. Math. with Appl. 75, 1582-1594.

 

 

A diffuse interface method was presented for simulating the evaporation process for a single bubble in a flow stream. The method was implemented using a least-squares finite-element method. A model for taking into account evaporation effects was implemented as a volumetric source term taking advantage of the diffuse interface formulation used for the simulation

La Forgia N., Fernandino M., Dorao C.A. (2014). Numerical simulation of evaporation process of two-phase flow in small-diameter channels. Heat Transfer Engineering, 35, 440-451.

 
 
 
 
 

 

Fractional derivatives provide a general approach for modeling transport phenomena occurring in diverse fields. In this article, the Least Squares Spectral Method is applied for solving advection–dispersion equations using Caputo or Riemann–Liouville fractional derivatives.

 

Carella, A.R., Dorao, C.A. (2013). Least-Squares Spectral Method for the solution of a fractional advection-dispersion equation. Journal of Computational Physics, 232(1), 33-45.

Publications

Kwakkel M., Fernandino M., Dorao C.A. (2020). A redefined energy functional to prevent mass loss in phase-field methods. AIP Advances 10, 065124.

Park K., Dorao C.A., Fernandino M. (2018). Thermal two-phase flow with a phase field method. Int. J. Multiphase Flow 100, 77-85.

Park K., Gerritsma M., Fernandino M. (2018). C1 continuous h-adaptive least-squares spectral element method for phase field models. Comp. Math. with Appl. 75, 1582-1594.

Park K., Fernandino M., Dorao C.A., Gerritsma M. (2017). The least-squares spectral element method for phase-field models for isothermal fluid mixture. Comp. Math. with Appl. 74., 1981-1998.

Park K., Fernandino M., Dorao C.A. (2016). Numerical solution of incompressible Cahn-Hilliard and Navier-Stokes system with large density and viscosity ratio using the least-squares spectral element method. J. Fluid Flow, Heat and Mass Transfer 3, 73-85.

Deng H, Fernandino M., Dorao C.A. (2015). A numerical investigation of flow boiling of non-azeotropic and near-azeotropic binary mixtures. Int. J. of Refrigeration, 49, 99-109.

Deng H, Fernandino M., Dorao C.A. (2015). Modeling of annular-mist flow during mixtures boiling. Applied Thermal Engineering, 91, 463-470.

Deng H., Fernandino M., Dorao C.A. (2014). Numerical study of heat and mass transfer of binary mixtures condensation in mini-channels. Int. Comm. Heat and Mass Transfer, 58, 45-53.

La Forgia N., Fernandino M., Dorao C.A. (2014). Numerical simulation of evaporation process of two-phase flow in small-diameter channels. Heat Transfer Engineering, 35, 440-451.

Carella, A.R., Dorao, C.A. (2013) View Correspondence (jump link) Least-Squares Spectral Method for the solution of a fractional advection-dispersion equation. Journal of Computational Physics, 232(1), 33-45.

Manavela Chiapero E., Fernandino M., Dorao C.A. (2013). Numerical analysis of pressure drop oscillations in parallel channels. Int. J. Multiphase Flow, 56, 15-24.

Manavela Chiapero E., Fernandino M., Dorao C.A. (2013). On the influence of heat flux updating during pressure drop oscillations – A numerical analysis. Int. J. Heat and Mass Transfer, 63, 31-40.

Ruspini L.C., Dorao C.A., Fernandino M. (2011). Simulation of a natural circulation loop using a least squares hp-adaptive solver, Mathematics and Computers in Simulation, 81(11), 2517-2528.el. Experimental Thermal and Fluid Science 83, 78-87.

Fernandino M., Dorao C.A. (2011). The least squares spectral element method for the Cahn-Hilliard equation, Appl. Math. Modell., 35(2), 797-806.

Dorao, C.A. (2011). Simulation of thermal disturbances with finite wave speeds using a high order method. Journal of Computational and Applied Mathematics, 231(2), 637-647.

Dorao C.A., Fernandino M., Jakobsen H.A., Svendsen H.F. (2009). hp-adaptive spectral element solver for reactor modelling, Chem. Eng. Science, vol. 64(5), pp. 904-911.

Fernandino M., Dorao C.A., Jakobsen H.A. (2007). Jacobi Galerkin Spectral Method for Cylindrical and Spherical Geometries, Chemical Engineering Science, Vol. 62 (23), pp. 6777-6783.

Dorao, C.A., Jakobsen, H.A. (2007). A parallel time-space least squares spectral method for incompressible flow problems. Applied Mathematics and Computation, 185(1), 45-58.

 

PhD Thesis

Keunsoo Park, (2017). Phase-field models for two-phase flows using the least-squares method. Supervisor: Maria Fernandino.

Nicolas La Forgia, (2014). Experimental facility design and a diffuse interface numerical model for studying evaporating bubbles in mini-channels. Supervisor: Maria Fernandino.

MSc Thesis

Luis Ugueto, (2013). Experimental Study of Density Wave Oscillations. MSc Thesis. NTNU.

Dejan Doder, (2013). Experimental analysis of the pressure characteristic cruve of a forced convection boiling flow in horizontal channel. MSc Thesis. NTNU.

Dag Stromsvag, (2011). Fundamental mechanisms of density wave oscillations and the effect of subcooling. MSc Thesis. NTNU.